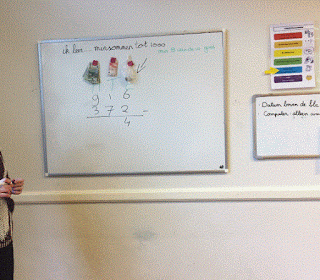Rekenspel 176 Vakantie tossen

Een meegevertje: Koop voor alle kinderen van de school een spel kaarten. Kopieer een van de onderstaande spellen op een kaartje en geef dit de kinderen mee.
Doe er een Rekenbingo kaart bij. Wie de bingokaart vol heeft krijgt na de vakantie een beloning. Bv een kwartier een spel voor de groep kiezen...

Vakantie tossen - gewoon

Je mengt de twee stapels kaarten door elkaar en krijgt elke speler de helft. Het is de bedoeling dat de spelers beide één kaart omdraaien. Degene met de hoogste kaart wint en krijgt beide kaarten. Dit herhaalt zich tot een van de spelers geen kaarten meer heeft. Wanneer beide kinderen trouwens dezelfde waarde omdraaien, dan moeten ze beide een stapeltje van drie kaarten afpakken en daar de bovenste van omdraaien. Wie nu de hoogste kaart heeft, krijgt alle acht de kaarten.

Dit spel is geschikt om kinderen met het concept 'meer, minder of gelijk' te laten oefenen (groep 1 en 2).

Vakantie tossen - plus

Je speelt het spel ongeveer hetzelfde, alleen draaien de spelers nu niet één, maar twee kaarten om. De winnaar is nu degene waarbij de som van beide kaarten het hoogst is. Bij een even hoge som, geldt ook hier dat er drie kaarten ingezet moeten worden, waarvan de bovenste twee omgedraaid worden. De hoogste som daarvan wint. Je zou het spel ook met minsommen kunnen spelen.

Dit spel is geschikt om kinderen de min- en plussommen onder de twintig te laten oefenen (groep 3 en 4).

Vakantie tossen - keer

Je speelt het spel ongeveer hetzelfde, alleen draaien de spelers nu niet één, maar twee kaarten om. De winnaar is nu degene waarbij het product van beide kaarten het hoogst is. Bij een even hoog product, geldt ook hier dat er drie kaarten ingezet moeten worden, waarvan de bovenste twee omgedraaid worden. Het hoogste product daarvan wint.

Dit spel is geschikt om kinderen de tafeltjes te laten automatiseren (groep 5 en 6).

Vakantie - mix

Het verschil bij dit spel is dat je hier telkens drie kaarten omdraait. Voorafgaand spreken de spelers bewerkingen af, bijvoorbeeld 'min en plus' of 'plus en keer'. Ze moeten de drie omgedraaide kaarten dan zo neerleggen dat de score het hoogst is. Bijvoorbeeld: 3x5+7 is minder waard dan 7x5+3.

Dit spel is geschikt voor het oefenen met de volgorde van bewerkingen (groep 7 en 8).

Klik hier voor de link van een BINGO kaart in de words versie
Klik hier voor de link van een BINGO kaart in de PDFversie
Naar een idee van JUF LISA

Tip: stappenplan redactiesommen

Gezien op internet: Stappenplan voor redactie sommen. 
Voor zwakke rekenaar belangrijk om structuur te hebben. Ik adviseer leerfkrachten ook altijd om dit stappenplan zichtbaar op te hangen in hun groep.

Klik hier voor de link!

Gezien: inwisselen met geld bij aftrekken van sommen onder elkaar

Gezien op een school: de stappen van het handelingsmodel op het school bord! 

Wanneer de CITO-lvs toetsen zijn afgerond is het vaak handig om een analyse te maken van de fouten. Door te onderzoeken in welke categorieën een leerling fouten maakt kun je je onderwijs beter aanpassen aan de leerling. Uiteraard naast het gebruik van het drielsagmodel tijdens je lessen en je verlengde instructie, zodat je ziet waar de hapering bij de kinderen begint.

De makers van Nieuw leren hebben op hun website een tool staan om een Cito-analyse te maken. Zowel van de oude als van de 3.0 toetsen.

"Om het maken van deze analyse wat handiger te maken hebben we een tooltje ontwikkeld waarmee je per leerling makkelijk kunt zien hoeveel procent een leerling verkeerd heeft gemaakt bij elke categorie. We vermelden ook het aantal sommen in die categorie zodat je een goed beeld krijgt van hoe de leerling de CITO heeft gemaakt."

Bron: www.nieuwleren.nl/

Klik hier voor de link.

Tafels flitsen

Tafels flitsen van de site van Juf Lisa

Met deze presentaties kun je flitsen op het bord. De sommen zijn groot, dus alle leerlingen kunnen het goed zien. Ook zijn er presentaties bij waarin de sommen afgewisseld worden aangeboden




Klik hier voor de site.

(Hieronder staan ze geüpload van de site van juf Lisa, zodat ik zeker weet dat ze te downloaden zijn! )

Klik hier om de presentatie van de tafel van 2 te downloaden.
Klik hier om de presentatie van de tafel van 3 te downloaden.
Klik hier om de presentatie van de tafel van 4 te downloaden.
Klik hier om de presentatie van de tafel van 5 te downloaden.
Klik hier om de presentatie van de tafel van 6 te downloaden.
Klik hier om de presentatie van de tafel van 7 te downloaden.
Klik hier om de presentatie van de tafel van 8 te downloaden.
Klik hier om de presentatie van de tafel van 9 te downloaden.
Klik hier om de presentatie van de tafel van 10 te downloaden.
Klik hier om de presentatie van tafels 2, 3, 4 en 5 te downloaden.
Klik hier om de presentatie van tafels 6, 7, 8 en 9 te downloaden.

Klik hier om de presentatie van alle tafels te downloaden.

Berekeningen opschrijven!

Mooie tip voor het nieuwe schooljaar!  Laat berekeningen opschrijven.
Natuurlijk wisten we dit al. Maar nu is hier iemand op gepromoveerd.

Zwakke rekenaars uit groep 8 presteren beter als ze bij ingewikkelde sommen de berekeningen opschrijven. Dat ontdekte psycholoog Marije Fagginger Auer. De specialist in Methodologie en Statistiek ziet perspectief: ‘Na een training kiezen deze leerlingen vaker voor deze oplossingsstrategie.’ 

Het rekenniveau van leerlingen in groep 8 is de afgelopen decennia op bepaalde onderdelen sterk gedaald, in het bijzonder bij vermenigvuldigen en delen met meercijferige getallen (bijvoorbeeld 23×56 en 544÷34). Dit hangt samen met veranderingen in de strategieën die leerlingen gebruiken om opgaven op te lossen: leerlingen beantwoorden vaker opgaven zonder daarbij een berekening te noteren en ze maken daarbij veel fouten. Promovenda Fagginger Auer: ‘We wilden meer inzicht krijgen in deze ontwikkelingen en in mogelijke oplossingen. Ons onderzoek laat zien hoe belangrijk het is om de oplossingsstrategieën van kinderen te bestuderen. Ook toont het aan dat kinderen baat kunnen hebben bij het opschrijven van hun berekeningen, vooral de kwetsbare groep zwakkere rekenaars.’

Klik hier voor het hele artikel.

Klik hier voor de link voor een luisterfragment  met Marije Fagginger Auer

Als kinderen blijven tellen.....deel 5 10 Tips en suggesties

Dit is het laatste artikeltje uit de reeks "Als kinderen blijven tellen". Voorgaande artikelen gingen in op het ontstaan van dit probleem en wat je als leerkracht hier tegen kan doen. In dit artikel zetten we de hoofdzaken nog eens op een rijtje.

1. Geef kinderen meer tijd. Sommige kinderen hebben nu eenmaal meer tijd nodig om dit te oefenen.

2. Oefen expliciet het opzetten van getallen, aflezen van getallen en het inslijpen van getalbeelden met flitskaarten

3. Optellen en aftrekken met het rekenrek met als doel dat kinderen kunnen redeneren op basis van getalrelaties:

1. doen: handelen op het rekenrek ( niet tellend maar schuivend met aantallen)
2. kijken: kijken naar het rekenrek
3. voorstellen: denken aan het rekenrek

4. De basisstrategieën voor het rekenen tot 20 is het rekenen via de 10 bijvoorbeeld: 8 + 7; eerst 2 erbij en dan 5. Belangrijk hierbij is het gebruik van het rekenrek. Bespreek met de leerlingen waarom de 7 gesplitst wordt in 2 en 5 en niet in bijvoorbeeld 1 en 6. Maak hierbij de koppeling met de ‘vriendjes van 10’ (of de ‘verliefde harten’).

5. Maak de strategieën voor het rekenen tot 10 (nog eens) expliciet:

1. Doortellen : erbij 1, bijv. 4 + 1 . Erbij 2 , bijv. 4 + 2
2. Vijfsommen : Bijv. 5 + 4 , 5 + 3
3. Vriendjes van 10 (aanvullen tot 10) : Bijv. 9 +1, 8 + 2
4. (Bijna)dubbelen : Bijv. 4+4, 4+3
5. Verwisselen : 1+7 wordt 7+1

En bij het aftrekken t/m 10:

1. Terugtellen : eraf 1, bijv. 7 – 1. Eraf 2, bijv. 7 – 2
2. Vijfsommen : 9 – 4, 9 – 5, 8 – 3, 8 – 5
3. Vriendjes van 10 : Bijv. 10 – 8, 10 – 4, 10 – 7
4. (Bijna) verdwijnsommen : Bijv. 8-8, 9-8, 7-6
Sommen die overblijven en apart aandacht verdienen zijn: 6+3, 7–3 en 9–6

7. De transfer leggen van de structuren (getalbeelden) naar de strategieën voor de sommen en gebruik maken van materiaal zoals vingerbeelden, rekenrek en eierdozen.

8. Bespreek expliciet met kinderen het doel van het proces: waarom is dit nodig. Bespreek ook steeds de tussen stappen, zodat kinderen zien dat ze groeien.

9. Geef rekendictee’s in een oplopend straf tempo.

10. Gebruik computers programma’s of app die stimuleren tot het in een keer geven van een antwoord.

Bron: 

http://www.masterplandyscalculie.nl/docs/po-automatiseren-en-memoriseren-van-het-rekenen-ine-van-der-sluis.pdf  ( geraadpleegd op 24-02-2016)
http://www.fi.uu.nl/toepassingen/01042/documents/katern_structureren_helpt_lessen.pdf (geraadpleegd op 24-02-2016)
http://www.fi.uu.nl/publicaties/literatuur/2008_onderwijsexperiment_fenna_van_nes.pdf (geraadpleegd op 24-02-2016)
www.slo.nl
De With, de, J, Rekenprikjes  Uitgeverij CED, ISBN: 978-90-5819-273-8

Als kinderen blijven tellen.....deel 4 Automatiseren

Dit is het vierde artikel uit de reeks Als kinderen blijven tellen.

Het belang van automatiseren:

Onder automatiseren wordt verstaan het vrijwel routinematig uitvoeren van rekenhandelingen. Als kinderen de basisbewerkingen hebben geautomatiseerd, hoeven zij hun werkgeheugen minder te belasten bij het uitrekenen van complexere opgaven. Een groter deel van het geheugen blijft dan beschikbaar voor het uitvoeren van niet-geautomatiseerde rekenhandelingen.

Automatiseren is van belang voor het aanleren van vaardigheden die op een hoger cognitief niveau liggen. Rekenzwakke kinderen komen vaak moeilijk tot automatisering van basiskennis.  Hoewel automatismen niet voorwaardelijk zijn voor het leren rekenen, is het wel van essentieel belang voor het vlot leren rekenen. Dit is dus een van de grootste hobbels voor rekenzwakke kinderen.

Om kinderen die bij tellen te helpen bij het automatiseringsproces zijn de volgende stappen van belang:

1. Begripsvorming door veel tijd te besteden aan verkenning en oefenen van tellen en getalrelaties.
2. Begripsvorming door het oefenen van het structureren. Uiteraard stapsgewijs.
3. Uitleg van de strategie. Ook hier weer strategie voor strategie.
4. Het leren herkennen van de strategie(kleur de som met de strategie op een sommenblad )
5. Rekentempodictee met de strategie, met straftempo zodat tellen onmogelijk is. Van een strategie tot het gebruik van meerdere strategieën in een dictee.
6. Kinderen noteren op matrixblad welke sommen ze beheersen( klik hier voor een voorbeeld)
7. Evt. uitvallers dit extra laten oefenen met spelletjes(bv Haaibaai van www.slo.rekenspellen.nl)

In standaard programma dat hierbij kan helpen is het programma Rekenprikjes.
Rekenprikjes is een automatiserings- en memoriseringsprogramma voor het rekenen tot 20. Dit programma biedt een aanpak die gemakkelijk in de reguliere rekenles is in te bouwen en waarmee de valkuil van het tellend rekenen tijdig wordt gesignaleerd. 

In Rekenprikjes komen alle strategieën voor het automatiseren en memoriseren van het rekenen tot tien en met tientaloverschrijders aan bod. Door de gehanteerde systematiek zal tellend rekenen plaats maken voor zogenaamde rekenfeiten: het in een oogopslag 'zien' van aantallen en uitkomsten.

Rekenprikjes bevat veel en afwisselend oefenmateriaal. Door periodieke afname van de Diagnostische Automatiserings Toets kunnen hardnekkige problemen in een vroeg stadium worden opgespoord, en doelgericht worden aangepakt.

Het vijfde en laatste artikel in deze reeks sluit af met een 10 tal tips.

Als kinderen blijven tellen.....deel 3 Het werken met structuren

Dit is het derde artikel uit de reeks: Als kinderen blijven tellen.

Het werken met structureren en getalbeelden is een aanpak om het tellend rekenen af te bouwen. Daarbij gaat men in de loop van het leerproces steeds een stap verder, van materiaal naar model
Wat omvat het?
- het kunnen tellen tot 20 met sprongetjes van 2 en 5
- structuur aanbrengen door samennemen en splitsen van hoeveelheden
- leren herkennen van getalbeelden tot 6 (dobbelbeelden)
- leren opzetten en herkennen van vingerbeelden tot 10
- structureren van hoeveelheden tot 10 op basis van (bijna)dubbelen en vijfstructuur
- het leren splitsen en aanvullen van hoeveelheden en getallen tot 10
- uitbreiden tot 20, waarbij naast de vijfstructuur ook de structuur van tien aan de orde komt

In de katern "Structureren helpt lessen" (Freudental) staan een aantal voorbeelden van structuren:

Vingers:

Veel kinderen gebruiken de vingers van nature, maar dan meestal één voor één tellend. In het reken-wiskundeonderwijs kan van vingers gebruikgemaakt worden om getallen en getalrelaties tot tien te verkennen. We hebben immers vijf vingers aan één hand, die hoef je dus niet steeds opnieuw te tellen. Dat lijkt voor ons volwassenen vanzelfsprekend, maar voor zwakke rekenaaars geldt dit niet. Zij tellen meestal wel steeds opnieuw en vaak is dat tellen ook nog niet synchroon, waardoor ze steeds weer tot een ander aantal komen. Soms is er onduidelijkheid over de duim: is dat een vinger of niet? Voor deze leerlingen moet er in het onderwijs expliciet aandacht worden besteed aan het feit dat er vijf vingers aan één hand zitten.

Pas als het kind begrijpt dat de vijf vingers een eenheid zijn, kan daarvan gebruikgemaakt worden in het opzetten van andere aantallen: 8 als 5 en 3, 9 als 5 en 4 enzovoort.

De volle hand die staat voor ‘vijf’ staat daarbij centraal en dient ter verkenning van getallen en getalrelaties. Zo wordt acht bijvoorbeeld een volle hand (vijf) en nog drie; zeven een volle hand (vijf) en nog twee enzovoort. Het verwoorden van het beeld is erg belangrijk, om kinderen te leren vertrouwen op de getallen

Rekenrek:

Ook met het rekenrek wordt ingespeeld op de noodzaak structuur aan te brengen in een hoeveelheid. Het rekenrek bevat de vijfstructuur en sluit in die zin goed aan bij het rekenen met de vijf vingers aan één hand. Voor zwakke rekenaars is van belang dat die link duidelijk wordt gelegd: Vijf vingers aan de ene hand,  vijf rode kralen;
vijf vingers aan de andere hand,  vijf witte kralen.
Samen tien vingers, tien kralen.
Het rekenrek is een goed middel om kinderen het nut van getalbeelden te leren, mits de link wordt gelegd met wat al bekend is. Bovendien kan het rekenrek gebruikt worden om strategieën, zoals dubbelen en bijna dubbelen te verkennen, bijvoorbeeld

Het rekenrek kent ook nadelen:

Het rekenrek kan beter niet worden gebruikt als middel om sommen uit te rekenen. Voor het verkennen en leren beschrijven van getalbeelden en het bestuderen van strategieën is het een prima middel. Zodra kinderen sommen op het rek gaan maken loopt u echter het risico dat het een mechanisch geschuif met kralen wordt, terwijl het onderliggende inzicht ontbreekt.

Eierdoos
De eierdoos is een voorbeeld van materiaal uit de werkelijkheid waarin een vijf- en tienstructuur zit. Net als bij het rekenrek is het van belang dat er een verband wordt gelegd met wat het kind al weet, zoals bijvoorbeeld de vijf vingers aan een hand:

Vijf vingers aan een hand,
vijf eieren op een rijtje.
Het andere rijtje is net zolang, dus ook vijf eieren. Samen tien eieren (want tien vingers aan twee handen).

Grote voordeel boven het rekenrek is, dat  het bij de eierdoos mogelijk is om eieren op te pakken en te verplaatsen. De structuur van de eierdoos nodigt er zelfs sterk toe uit.

Mogelijkheid tot niveauverhoging
De dozen hebben als voordeel boven het rekenrek dat er transfer mogelijk is van het werken met zichtbare, telbare hoeveelheden naar het werken met getallen/cijfersymbolen. Een volle doos kan worden dichtgedaan. Je weet dan nog dat er tien eieren inzitten, want dat staat erop. Ook voor andere getallen kan een dergelijke aanpak werken. U kunt het aantal eieren dat in de doos zit bijvoorbeeld op een memoblaadje noteren en op de doos plakken. De feitelijke hoeveelheid zit nu letterlijk onder het getal. In geval van twijfel kan de doos worden geopend en krijgt de leerling zicht op zowel inhoud als structuur van het getal.

Turven
Een andere veelgebruikte manier om structuur aan te brengen in een hoeveelheid is het turven. Vaak wordt er geturfd als achteraf niet meer controleerbaar is wat het aantal was (bijvoorbeeld een hoeveelheid auto’s tellen gedurende een bepaalde periode of het aantal keren dat de juf het getal tien noemt bijhouden tijdens het voorlezen van een verhaaltje). Ook bij het turven wordt gebruikgemaakt van de vijfstructuur. De structuur zit er echter niet automatisch in, maar moet er door de leerlingen in aangebracht worden. Voordeel van turven is dat het ook voor grotere hoeveelheden kan worden gebruikt. Nadeel is dat het kind al moet begrijpen dat een streepje een voorwerp kan symboliseren, terwijl dat nu juist voor veel zwakke rekenaars een probleem is. Bovendien is het turven statisch: het is een weergave van een moment. Bij een nieuwe situatie moet je opnieuw beginnen

Het vierde artikel in deze reeks bespreekt de didactiek van het automatiseringsproces.

Als kinderen blijven tellen.....deel 2 Tellen en tellend rekenen

Dit is het tweede artikel uit de reeks: Als kinderen blijven tellen. 

Tellen en tellend rekenen is de veilige beginstrategie voor alle rekenaars. Om van rekenen te kunnen spreken moet de telrij, zowel mondeling als schriftelijk gekend zijn. Voor jonge kinderen bestaat de ontwikkeling van tellen en getalbegrip uit verschillende kennisfeiten, vaardigheden en inzichten zoals bijvoorbeeld:

· kennis:
- het kennen van de telwoorden en opzeggen van de telrij;
- het herkennen van getalbeelden, bijvoorbeeld: patronen op de dobbelsteen, opgestoken vingers, kleine hoeveelheden;
 - het kennen van getalsymbolen;
- het kennen van hoeveelheidbegrippen, bijvoorbeeld: meer, minder, evenveel, weinig, veel, minste, meeste, ervoor, erna, volgende, vorige; 

· vaardigheden:
 - het tellen van hoeveelheden;
- het vergelijken en ordenen van hoeveelheden;
- het verkort tellen; - het koppelen van hoeveelheden, telwoorden en getalsymbolen;
- het oplossen van eenvoudige optel-, aftrek- en splitsprobleempjes; 

· inzichten:
- het snappen dat je met tellen een hoeveelheid kunt bepalen;
- het snappen dat je hoeveelheden kunt vergelijken via één-één-verbinden of door ze te tellen;
- het snappen dat je kunt denken en redeneren over hoeveelheden via denken in en redeneren over getallen;
- het snappen dat je niet alles één voor één hoeft te tellen om het aantal te bepalen;
- het snappen dat het structureren van hoeveelheden een handige manier van tellen is;
- het snappen dat de grootte van hoeveelheden relatief is

Het is duidelijk dat het 'leren tellen' in al zijn facetten voor jonge kinderen hierbij een centrale plaats inneemt. Bij getalbegrip benadrukken we de verwevenheid en het gebruik van kennis, inzicht en vaardigheden in diverse toepassingssituaties. Tijdens spontane en meer geplande activiteiten thuis en op school komen kinderen in aanraking met zoveel verschillende (tel)situaties dat het getalbegrip zich geleidelijk aan ontwikkelt.

Het proces van tellen en getalbegrip verloopt als volgt:
· Van imiteren naar resultatief tellen;
· Van resultatief tellen naar verkort tellen;
· Van werken met aantallen naar denken over getallen;
· Vergelijken en ordenen;
· Telgetal en getalsymbool

Waar het fout gaat bij kinderen die blijven tellen is de stap van resultatief naar het verkort tellen en/of van het werken met aantallen naar het denken over aantallen. Voor rekenen in de voorstelling is structurering voorwaarde. (Sluis, 2013)

Om te voorkomen dat de kinderen teveel blijven vasthouden aan een 1-voor-1 telhandeling, kan de leerkracht de kinderen erop wijzen dat ze op zoek moeten gaan naar ‘slimme maniertjes’ waarmee ze handig en zo snel mogelijk te weten kunnen komen bijvoorbeeld hoeveel blokjes er op de tafel liggen of hoeveel stippen er op een kaart staan. Dit verwijst direct naar de context. Wat hierbij kan helpen is als de leerkracht de verschillende soorten structuren ter sprake brengt en de kinderen stimuleert om de structuren met elkaar te vergelijken. Wellicht dat de kinderen hierdoor ook zelf verbanden tussen de verschillende structuren gaan leggen en de structuren uiteindelijk in andere configuraties gaan herkennen. 

Kinderen die vooral bekend zijn met één type structuur (bijv. vingerbeelden), zouden op deze manier in aanraking kunnen komen met andere structuren (bijv. dobbelsteenstructuren) en een aanzet kunnen maken om hun kennis over bepaalde structuren te vertalen naar het herkennen en gebruikmaken van meerdere soorten structuren. Belangrijk is dat de kinderen gaan inzien dat een bepaalde hoeveelheid op meerdere manieren kan worden uitgebeeld en dat hier meerdere soorten structuren voor gebruikt kunnen worden. Wat hierbij kan helpen is bijvoorbeeld het programma als Miertje Manier (Nes, 2008) waarbij bovenstaande nadrukkelijk wordt geoefend.

In het derde artikel staat het werken met structuren centraal.

Als kinderen blijven tellen….. deel 1

Dit artikel is het eerste van een reeks over het blijven tellen van kinderen. In dit eerste artikel ga ik in op de oorzaken van dit fenomeen. De volgende artikelen gaan over de opbouw van het tellen, het belang van structureren en het automatiseren gericht op het voorkomen van het blijven tellen.

Als leerkracht kennen we ze allemaal. Kinderen die blijven tellen. Je kunt er raar van worden. Je doet zo je best als leerkracht, maar je krijgt ze maar niet van het tellen af. De vraag is hoe komt het en nog belangrijker: wat kun je er aan doen.

Het lastigste is dat we kinderen eerst leren tellen en vervolgens moeten ze de stap maken om hier weer mee te stoppen. Bij het rekenen tot tien is immers het streven om te komen tot memoriseren. Misschien goed om het eens op een rijtje te zetten waarom blijven tellen niet goed is en hoe het proces van tellen, tellend rekenen en rekenen nu verloopt.

Wat is er op tegen?

- Vinger-rekenen betekent tellen en verder tellen, het is geen optellen en aftrekken. De directe, mechanistische gerichtheid op tellen blokkeert het inzicht in: de relaties tussen getallen en bewerkingen en structuren. Er ontstaat geen inzicht in getalstructuren.|
- Het is omslachtig en daardoor soms onbetrouwbaar.
- Vinger-rekenen kost tijd en kinderen hebben daardoor een laag tempo.

Het is handiger om uit je hoofd te rekenen:
- Je rekent met sprongen; dit is optellen en aftrekken. 
- Met de juiste strategie, reken je nauwkeurig.
- Met de juiste strategie, reken je veel sneller

Waarom blijven kinderen dan toch tellen?

Een aantal factoren zijn gelegen in het kind zelf:
• De behoefte vast te houden aan een (schijn)zekerheid. In de ogen van het kind levert het tellen in elk geval een antwoord op en meestal zal dat ook wel goed zijn. Voor hen brengt verkort tellen in eerste instantie risico’s met zich mee en leidt aanvankelijk daardoor ook vaker tot een fout antwoord. Eén voor één tellen heeft een sterke controlefunctie voor kinderen; je kunt het altijd doen en het leidt altijd tot een antwoord. Dit geeft het kind een grote mate van emotionele zekerheid. Dit kan voor het kind een ijzersterke motivatie zijn om te blijven tellen. 

• Zo razendsnel kunnen tellen dat er geen directe noodzaak bestaat om een andere strategie te kiezen. 

• De structuren om ons heen niet kunnen zien er dus ook geen gebruik van maken. Dit geldt zowel voor bestaande structuren (denk bijvoorbeeld aan vingers, eierdozen, kratjes) als voor een zelf aan te brengen structuur. Het netjes in een patroon leggen van bijvoorbeeld fiches gebeurt dan niet spontaan. 

• Niet zien dat de structuur gebruikt kan worden (en hoe) bij het oplossen van een rekenprobleem. Zo kunnen sommige kinderen bijvoorbeeld wel handig rekenen op de vingers (ze kunnen zeven vingers herkennen als vijf en nog twee vingers), maar zodra de som 5+2 aan de orde is leggen zij niet automatisch de link naar het vingerbeeld. Een oefening waarin vingerbeelden worden geflitst staat voor hen los van een som waarin de vingerbeelden kunnen worden gebruikt.

Een aantal factoren zijn ook gelegen in het onderwijs:
• Leerkrachten die als kinderen het goede antwoord geven op een vraag, checken” Weet je het zeker”, bang als ze zijn dat kinderen gokken…. Dat leidt bij kinderen tot het automatiseren: ik moet voor de zekerheid altijd nog even tellen.

• De methodes gaan te snel in het automatiseringsproces: sommige kinderen hebben meer tijd nodig.

• Leerkrachten hebben onvoldoende didactische kennis als het gaat om het rekenproces.

• In het programma zit te weinig oefening van zwakke rekenaars om hoeveelheden in een  keer te benoemen en te weinig aandacht door de 5 structuur.

• Kinderen krijgen de gelegenheid om te tellen doordat ze niet op tempo sommen moeten maken.

In het volgende artikel in deze reeks wordt nader in gegaan op de fasen in het Tellen en Tellend rekenen.

Sterke rekenaars: Hou ze bij de les!

In 2014 heb ik een blog geschreven over het gebruik van de Taxonomie van Bloom n.a.v. een artikel in Volgens Bartjens. Dit blog is een hit, want het het meest gelezen bericht! In januari 2016 stond weer een zeer lezenswaardig artikel over sterke rekenaars van de hand van Suzanne Sjoers en ligt eigenlijk in de lijn van het artikel in 2014. Daarom zal ik het hier uitvoerig bespreken. 

“Sterke rekenaars worden wel ‘instructie-onafhankelijke rekenaars’ genoemd. Vaak brengen ze een deel van de rekenles buiten het lokaal door met verrijkingsmateriaal, wat zonder instructie tot demotivatie en onderpresteren kan leiden. Instructie zorgt ook bij sterke rekenaars voor groei: het opdoen van nieuwe kennis en het aanleren van nieuwe vaardigheden.”
Als voorbeeld begint Sjoers met een prachtig voorbeeld van een differentiatie bij een startopdracht tafelsommen oefenen. De sterke rekenaars in groep 6 kregen geen ‘gewone’ tafelsommen zoals de rest van de groep, maar tafelsommen met iets extra’s: wat is het dubbele van 5 × 9, of wat is de helft van 7 × 8? 

Sjoers hanteert twee uitgangspunten in dit artikel:

* Een aangepast rekenaanbod heeft een positief effect op de rekenprestaties van sterke rekenaars. Ook het clusteren van ontwikkelingsgelijken heeft een positief effect, met name clusteren binnen het klaslokaal bevordert de rekenprestaties van de sterke rekenaars. Verschillende studies hebben evenzo aangetoond dat de leerkracht een grotere invloed heeft op het leren van leerlingen dan welke variabele ook. De leerkracht is namelijk degene die rekenbetrokkenheid en rekenpassie bij de leerling op gang kan brengen (Boaler, 2015). Het grootste leereffect is dus daar te vinden waar de leerkracht is: in de rekenles.

* Onderzoek laat zien dat sterke leerlingen gebaat zijn bij instructie op maat (Kruteskii, 1976). Maar wat wordt dan met ‘instructie’ bedoeld? Het woordenboek omschrijft instructie als ‘uitleg, richtlijn voor hoe je iets moet doen, aanwijzing’. In ieder geval is er bij instructie sprake van contact. Contact tussen leerkracht en leerling(en) en in dit contact vindt uitwisseling plaats met ontwikkeling als doel. Instructie kan dan gaan over de ontwikkeling van rekenkennis, maar ook van rekenvaardigheden, vaardigheden als probleem oplossen, formuleren, noteren en onderbouwen.

In dit artikel pleit Sjoers voor dagelijkse instructie voor sterke rekenaars tijdens de rekenles in het lokaal. Ze heeft hiervoor een alternatief lesmodel ontwikkelt. 
Een belangrijk uitgangspunt van dit model is dat de leerkracht vertrouwen heeft in het kunnen van leerlingen: zwakke rekenaars en de middengroep zijn prima in staat zelfstandig de stof te verwerken. De leerkracht heeft immers tijdens de instructie en verlengde instructie door het stellen van vragen (Hollingsworth, Ybarra & Schmeier, 2015) voortdurend gecontroleerd of alle leerlingen de instructie hebben begrepen. Een ander belangrijk uitgangspunt van dit model is dat alle typen rekenaars op een vast moment in de les instructie krijgen en dat de instructie aan sterke rekenaars dus een vast onderdeel van elke rekenles is. Bij dit instructiemodel blijven de sterke rekenaars zich onderdeel van de groep voelen. De leerkracht kan bovendien zicht houden op het leerproces van de sterke rekenaar en via feedback bijsturen waar nodig.

Sterke rekenaars hebben volgens Sjoers wel instructie nodig, maar de vorm waarop verschilt bij de instructie  van andere kinderen. Ze noemt in haar artikel 4 manieren hoe de instructie dan verschilt:

1. de instructie is evaluerend 
Sterke rekenaars leggen makkelijk verbanden met bestaande kennis en maken grote denksprongen. Ze hebben daardoor minder instructie over de inhoud nodig: globale hints die leerlingen in de goede richting wijzen, zijn vaak voldoende. Daarnaast hebben sterke rekenaars een voorkeur voor ontdekkend leren. Wanneer de instructie aan de andere groepen begint, kun je sterke rekenaars vanwege deze eigenschappen een denkactiviteit geven waarmee ze de instructiestof zelf gaan ontdekken. Deze denkactiviteit is dan gekoppeld aan het lesdoel en is geformuleerd als een open vraag, bovenin de Taxonomie van Bloom: Welke mogelijkheden kun je bedenken om 9 × 14 visueel te maken?  

2. de instructie is verrijkend.
Aan het lesdoel voor de sterke rekenaars voeg je de ‘plus’ toe door te verbreden naar een ander rekenkundig onderwerp of door een toepassing van het concept te bedenken. Een goed pluslesdoel daagt de sterke rekenaar uit om zijn/haar creativiteit in te zetten. Bijvoorbeeld: doel : vermenigvuldigen (werkwoord) met het splitsen van een factor (concept): 6 × 14 = 6 × 10 + 6 × 4
Pluslesdoel: welke mogelijkheden kun je bedenken om 9 × 14 visueel te maken? 

3. de instructie sluit aan op de rekenontwikkeling van de sterke rekenaar
Sterke rekenaars zijn in staat om in het handelingsmodel snel op het formele rekenniveau te komen. Op het niveau onder het formele niveau (voorstellen - abstract) wordt een denkmodel aangereikt. Dit model is een hulpmiddel om de stap te maken van ‘voorstellen – concreet’ naar formeel rekenen. Voor een sterke rekenaar is dit hulpmodel vaak niet nodig en kan dit juist voor verwarring zorgen.

4. de instructie heeft aandacht voor hiaten, werktempo en vaardigheden
Sterke rekenaars zijn goed in staat zichzelf conceptueel begrip aan te leren. Hun rekenvaardigheden met dit concept blijven alleen ver achter als er geen expliciete aandacht wordt besteed aan de oplossingsstrategieën en er tijd is om daar voldoende mee te oefenen. Tijdens de instructie heeft de leerkracht de kans de oplossingsstrategieën te bespreken met de sterke rekenaars. Regelmatig worden hierbij niet efficiënte zelfbedachte oplossingsstrategieën gesignaleerd. Deze kunnen dan tijdig hersteld worden.

Schoolbreed de inzichten van Sjoers bespreken  en vervolgens leerkrachten ondersteunen en laten trainen om plusdoelen te formuleren gekoppeld aan het doel van de les, is een effectieve werkwijze om sterke rekenaars te kunnen bedienen in de reguliere rekenlessen! Kennis van de Taxonomie van Bloom is hierbij een goed hulpmiddel.

Klik hier voor een artikel over Rekenen met de Taxonomie van Bloom

Bron: Sjoers, S(2016) Sterke rekenaars hou ze bij de les, Volgens Bartjens jaargang 35(3), blz 22-25.

Aanvulling september 2017:
Suzanne Sjoer heeft ook over dit onderwerp een boek geschreven: "Sterke rekenaars" Klik hier voor  meer info.

Automatiseren en memoriseren ( deel 5)

Dit vijfde artikel in deze reeks gaat in op de vraag hoe je als leerkracht zicht kunt houden op waar kinderen nu precies staan.

In het artikel uit Volgens Bartjens over Rekendrempels nemen( Danhof e.a. 2014) worden de profieltoetsen Rekenen besproken. Deze zijn ontwikkeld en gebruikt voor een onderzoek naar het ontstaan van rekenproblemen. En zijn geschikt om te onderzoeken hoe het er voor staat met het automatiseren.

Er wordt uitgegaan van  2 soorten toetsen:
1. screeningstoetsen die bestaan uit representatieve sommen op het niveau van de groepen 3 t/m 7 van het basisonderwijs
2. automatiseringstoetsen, waarmee de vlotte beschikbaarheid van de basiskennis voor het hoofdrekenen wordt getoetst

De screeningstoetsen brengen het kunnen oplossen van de sommen (we noemen dit ‘power’) in beeld, de automatiseringstoetsen zijn gericht op het kennen (‘speed’).

1.Power – de Screeningstoets – als aanvullend hulpmiddel voor de risicogroep. De screeningstoetsen bestaan uit representatieve sommen op het niveau van de groepen 3 tot en met 7 van het basisonderwijs. Ze kunnen aanvullend naast de methodetoetsen en de Cito-toetsen worden gebruikt. De screeningstoets biedt de leerkracht snel een systematisch beeld van achterstanden, hiaten en foutenpatronen. Op basis van het groepsoverzicht of de individuele Profielkaart kunnen nadere observaties en doelen voor herhaalde instructie en oefening worden gepland.

2 Speed – de Automatiseringstoetsen – preventieve functie voor de hele school. De automatiseringstoetsen, meten de vlotte beschikbaarheid van de basiskennis voor het hoofdrekenen. Deze toetsen vormen de kern van het programma. Ze geven de mogelijkheid automatiseringstekorten vroegtijdig te signaleren. Binnen dit project betekent automatiseren: meteen weten. Dit in tegenstelling tot in sommige andere publicaties waarbij ‘automatiseren’ slaat op ‘vlot kunnen uitrekenen’ en memoriseren op ‘meteen weten’. De automatiseringstoetsen (speedtoetsen) zijn eenvoudig af te nemen en verschaffen belangrijke informatie.

De ontwikkelaars van deze toetsen gaan er van uit rekenen stapelen is. Op een eigen profielkaart kan inzichtelijk worden gemaakt hoe de rekenmuur van het kind er voor staat.

Bron:
Danhof, e.a. 2014 Rekendrempels nemen: een goede basis voor het leren hoofdrekenen, Volgens Bartjens jaargang 34 2014/2015, pp 4 - 7
http://www.bareka.nl/  ( hier zijn de toetsen gratis te downloaden)

Automatiseren en memoriseren ( deel 4)

Dit is inmiddels het vierde artikel uit deze reeks. In de vorige artikelen is het verschil tussen automatiseren en memoriseren besproken en hoe de leerkracht dit kan oefenen in de groep. Dit artikel beschrijft welke sommen behoren tot de basiskennis en hoe dit verder geoefend kan worden.

De sommen die de basiskennis vormen, zijn verdeeld over vijf zogenaamde rekendrempels:

Drempel 1: optellen, aftrekken en splitsen tot en met 10, bijvoorbeeld: 4 + 3, 7 − 4, 

8 splitsen in 5 en 3 

Drempel 2: vlot kunnen ‘springen’ op de getallenlijn tot 100.
Drempel 3: optellen en aftrekken over 10 (tot 20), bijvoorbeeld: 8 + 7, 15 − 7.
Drempel 4: bouwsteensommen tot 100, zoals: 47 + 30 en 77 − 30, 28 + 7 en 35 − 7.
Drempel 5: eenvoudige tafels: 2, 3, 4, 5 en moeilijke tafels: 6, 7, 8, 9.

Het vlot kennen (goed beheersen) van de drempels draagt echter in sterke mate bij aan het kunnen oplossen van steeds moeilijker sommen. Tekorten in de basiskennis veroorzaken achterstanden en stagnatie. Anders gezegd: rekenen is stapelen! Voor de leerkracht is het van groot belang zicht te krijgen en te houden op de onderliggende lagen van het muurtje. Rekenproblemen worden vaak veroorzaakt doordat de onderliggende lagen in het rekenmuurtje niet stevig genoeg zijn! Dus niet genoeg zijn geautomatiseerd.

Het is belangrijk het voor het leren van leerlingen, dat ze weten wat ze moeten leren en waarom. (Hattie, 2008) Dat ze weten waar ze ongeveer staan én weten hoe ze zelf verder kunnen werken om hun doelen te bereiken. Als leerlingen meer grip hebben op hun eigen leren en zelf een actieve rol hebben, waarbij  ze niet afhankelijk van de 


leraar zijn, neemt hun motivatie toe. Ook groeit hun zelfvertrouwen als ze zien dat ze vorderingen maken en beseffen dat dat door eigen inspanning komt. Leerlingen die hoge, maar wel realistische, verwachtingen van zichzelf hebben blijken véél hoger te presteren dan wanneer ze geen, of lage verwachtingen hebben.

De SLO heeft Drempelkaarten gemaakt waarop kinderen zelf hun vorderingen kunnen bij houden. Maar ook een serie spellen uitgezocht en uitgewerkt die kunnen gebruikt om extra te oefenen bij het automatiseren en het onderhouden van de geautomatiseerde sommen en precies aansluiten bij de verschillende drempels.

Hattie, J, Visible Learning, Taylor & Francis Ltd,  2008

http://rekenspel.slo.nl/

,

Automatiseren en memoriseren (deel 3)

Dit artikel is een onderdeel uit een reeks over het belang van automatiseren en memoriseren. 

Volgens Gert Gelderblom ( 2007, Effectief omgaan met zwakke rekenaars)  draagt veelvuldig oefenen er in belangrijke mate toe bij dat rekenvaardigheden zich in het brein hechten. Volgens hem moet de rekenles altijd met een korte en felle automatiseringsoefening beginnen.

In de Handelingswijzer van Expertis  hanteert men de 7 A’s
· Alle dagen – beter alle dagen even 5 minuten, dan 1 keer per week een half uur 
· Alle kinderen – iedereen doet met de oefening mee 
· Aansluiten bij niveau – dicht bij het beheersingsniveau van de kinderen blijven 
· Aanmoedigen tot verkorten – in de feedback wijzen op korte denkstappen 
· Aantrekkelijke werkvorm – interactieve werkvormen zijn succesvol 
· Afwisselende inhoud – wissel het optellen, aftrekken, delen, vermenigvuldigen regelmatig af in verschillende oefenmomenten (niet alles in 1 oefenmoment proppen) 
· Veel interActie – stimuleer het samenwerken tussen kinderen

Als de automatisering goed op gang is gekomen is onderhoud door spelvormen al dan niet met behulp van coöperatieve werkvormen een volgende stap. 
In het artikel “Het effect van gericht automatiseren van rekenvaardigheden”  van de site www.wij-leren.nl  beschrijft Marjolijn Zwik dat dagelijkse aandacht (5 à 10 minuten) voor automatisering met behulp van coöperatieve werkvormen en digitale werkvormen op het digitale schoolbord aantoonbaar leidt tot betere rekenresultaten.  Spellen over de getallenlijn, twee dobbelstenen optellen, drie dobbelstenen optellen, Minsommen flitsen, plussommen flitsen, optellen met getallenkaartjes, plofsommen tot 100, splitsen, dobbelen met meerdere dobbelstenen, gooi met één, twee of drie dobbelstenen.
De structuren uit Structureel Coöperatief Leren(Kagan,2009) die volgens haar geschikt zijn:
•    Binnen/Buitenkring
•    Flitskaarten
•    Genummerde Koppen Bij Elkaar
•    Mix & Koppel
•    Tweetal Coach
•    TweeVergelijk
•    Schud & Pak

De meeste spellen op deze site lenen zich hier natuurlijk ook voor!


Bron:
Handelingswijzer automatiseren Expertis  klik hier
Masterplan Dyslcalculie CED 
www.wij-leren.nl /Het effect van gericht automatiseren van rekenvaardigheden

Automatiseren en memoriseren (deel 2)

Dit is een vervolg op het artikel  Automatiseren en memoriseren (deel 1)

Memoriseren tot 10 is de basis voor de volgende sommen:

1.Tientaloverschrijders (splitsen)
2. Relatie kleine en grote opgaven  5+3  50+ 30   500+300
3. Kolomsgewijs of cijferend optellen en aftrekken
4. Handig rekenen

Kinderen komen slecht tot memoriseren, doordat ze blijven tellen en de kans ook krijgen om te blijven tellen. Waarom is blijven tellen dan slecht? Er ontstaat geen opbouw van getalbegrip en het tempo blijft laag.  Verder blokkeert de gerichtheid op tellen het inzicht in de relaties tussen getallen en bewerkingen en structuren.

Voorbeeld van relaties tussen getallen:

7 + 8 en 7 + 7
9 - 8 en  9 - 9
1 + 7 en 7 + 1

Bij het rekenonderwijs moet voor dit proces dus meer aandacht  zijn. De didactiek van het automatiseren zou dus niet alleen op het inprenten (drill en practice) gericht moeten zijn.  Bijvoorbeeld de oude manier van tafels leren:” Leer de tafels als een opzegversje, dan komt het wel goed”.

Kinderen moeten eerst succesvolle strategieën aangeleerd krijgen. Vervolgens oefenen met de juiste effectieve strategie en dan steeds het tempo verhogen, zodat tellen onmogelijk is.

Succesvolle strategieën zijn:

Sommige mensen vragen zich af: staat dit dan niet in de methode. Soms wel, maar soms ook erg versluierd, zodat leerkrachten deze niet goed herkennen.  De strategieën moet structureel worden ingeoefend.

Stappenplan
1. Uitleg van de strategie
2. Herkennen van de strategie(kleur de som met de strategie op een sommenblad )
3. Rekentempodictee met de strategie, met straftempo zodat tellen onmogelijk is
4. Kinderen noteren op matrixblad welke sommen ze beheersen( klik hier voor een voorbeeld)
5. Evt. uitvallers dit extra laten oefenen met spelletjes(bv Haaibaai)

De stappen van het stappenplan verdelen over 14 dagen en elke stap regelmatig herhalen. U moet dit zien als korte oefensessies van 3 tot 5 minuten. Als de strategie goed zit, kan het automatiseren op snelheid beginnen. Vervolgens oefent u de volgende strategie. Onderhoud door regelmatig rekentempodictees en 3 minutenoefeningen met sommenbladen. (25 sommen per minuut is de norm).

klik hier voor een werkblad sommengenerator

Automatiseren en memoriseren (deel 1)

Automatiseren en memoriseren zijn begrippen die vaak worden gebruikt in het onderwijs. In de praktijk merk ik dat niet iedereen precies weet wat hiermee wordt bedoeld. Dat betekent dat leerkrachten soms maar wat doen als het gaat om kinderen te helpen bij deze processen tijdens het rekenen.

De definitie van de beide begrippen:

Memoriseren is direct beschikbare kennis van rekenfeiten. Het kind weet het antwoord op de som gewoon. Hoeft niet meer te denken aan een beeld of strategie. Bij het rekenen tot tien en de tafels  is het streven om te komen tot memoriseren.

Automatiseren is het proces van verkorting van oplossingsmethoden. Het kind hoeft niet na te denken over de volgende tussenstap. Hiervoor moeten de tussenstappen rekenfeiten zijn (gememoriseerd). Bijvoorbeeld bij het oplossen van sommen door het tiental gebruik te maken van de strategie ‘eerst naar de 10’

Het belang van automatiseren:

Onder automatiseren wordt verstaan het vrijwel routinematig uitvoeren van rekenhandelingen. Als kinderen de basisbewerkingen hebben geautomatiseerd, hoeven zij hun werkgeheugen minder te belasten bij het uitrekenen van complexere opgaven. Een groter deel van het geheugen blijft dan beschikbaar voor het uitvoeren van niet-geautomatiseerde rekenhandelingen.

Automatiseren is van belang voor het aanleren van vaardigheden die op een hoger cognitief niveau liggen. Rekenzwakke kinderen komen vaak moeilijk tot automatisering van basiskennis.  Hoewel automatismen niet voorwaardelijk zijn voor het leren rekenen, is het wel van essentieel belang voor het vlot leren rekenen. Dit is dus een van de grootste hobbels voor rekenzwakke kinderen.

Als kinderen de basisbewerkingen hebben geautomatiseerd, hoeven zij hun werkgeheugen minder te belasten bij het uitrekenen van complexere opgaven. Een groter deel van het geheugen blijft dan beschikbaar voor het uitvoeren van niet-geautomatiseerde rekenhandelingen.

Als het gaat om hoe het rekenproces verloopt, hebben we het eerst over verkennen van het geleerde(begrip), daarna over het oefenen van het geleerde, dan het automatiseren van het geleerde en tot slot ontstaat dan dat het geleerde is gememoriseerd.  Er kan nu vlot gerekend worden en in andere situaties worden toegepast.